1. Basics
1.1 A First Example
The following program can be compiled and linked
with LEDA's basic library libL.a (cf. section 1.10).
When executed it reads a sequence of strings from the standard input and then
prints the number of occurrences of each string on the standard output. More
examples of LEDA programs can be found throughout this manual.
#include LEDA/d_array.h
main()
{ &
&d_arraystring,int N(0);
&string s;
&while &(cin s ) N[s]++;
&forall_defined(s, N)
cout s " " N[s] endl;
}
The program above uses the parameterized data type dictionary array
(
d I, E) from the library. This is expressed by the include
statement (cf. section 1.9 for more details). The specification of the
data type d
I, E) from the library. This is expressed by the include
statement (cf. section 1.9 for more details). The specification of the
data type d can be found in section 4.4. We use it also as a
running example to discuss the principles underlying LEDA in sections 1.2
to 1.10.
can be found in section 4.4. We use it also as a
running example to discuss the principles underlying LEDA in sections 1.2
to 1.10.
Parameterized data types in LEDA are realized by templates,
inheritance and dynamic binding (see [N92] for details).
For compilers not supporting templates there is still available a
non-template version of LEDA using declare macros as described in [N90].
1.2 Specifications
In general the specification of a LEDA data type consists of four parts:
a definition of the set of objects comprising the (parameterized) abstract
data type, a description of how to create an object of the data type,
the definition of the operations available on the objects of the data
type, and finally, information about the implementation. The four parts
appear under the headers definition, creation, operations, and implementation
respectively.
• Definition
This part of the specification defines the objects (also called instances or
elements) comprising the data type using standard mathematical concepts and
notation.
Example, the generic data type dictionary array:
An object a of type
d I, E is an injective function from the
data type I to the set of variables of data type E. The types I and
E are called the index and the element type respectively, a is called
a dictionary array from I to E.
I, E is an injective function from the
data type I to the set of variables of data type E. The types I and
E are called the index and the element type respectively, a is called
a dictionary array from I to E.
Note that the types I and E are parameters in the definition above.
Any built-in, pointer, item, or user-defined class type T can be used
as actual type parameter of a parameterized data type. Class types however
have to provide the following operations:
a) &a constructor taking no arguments
&T::T()
b) &a copy constructor &T::T(const T&)
c) &an input function &void Read(T&, istream&)
d) &an output function &void Print(const T&, ostream&)
A compare function ``int compare(const T&, const T&)" (cf. section 1.6)
has to be defined if the data type requires that T is linearly ordered.
Section 1.4 contains a complete example.
• Creation
A variable of a data type is introduced by a variable declaration.
For all LEDA data types variables are initialized at the time of declaration.
In many cases the user has to provide arguments used for the initialization
of the variable. In general a declaration
XYZt1,..., tk
y(x1,..., x );
);
introduces a variable y of the data type ``
XYZt1,..., tk''
and uses the arguments
x1,..., x to initialize it. For example,
to initialize it. For example,
d string, int A(0)
string, int A(0)
introduces A as a dictionary array from strings to integers, and
initializes A as follows: an injective function a from string
to the set of unused variables of type int is constructed, and is
assigned to A. Moreover, all variables in the range of a are
initialized to 0.
The reader may wonder how LEDA handles an array of infinite size. The
solution is, of course, that only that part of A is explicitly stored
which has been accessed already.
For all data types, the assignment operator (=) is available for variables
of that type. Note however that assignment is in general not a constant time
operation, e.g., if L1 and L2 are variables of type listT then the
assignment L1 = L2 takes time proportional to the length of the list L2
times the time required for copying an object of type T.
Remark: For most of the complex data types of LEDA, e.g., dictionaries,
lists, and priority queues, it is convenient to interpret a variable name
as the name for an object of the data type which evolves over time by means
of the operations applied to it. This is appropriate, whenever the operations
on a data type only ``modify'' the values of variables, e.g., it is more
natural to say an operation on a dictionary D modifies D than to say that
it takes the old value of D, constructs a new dictionary out of it, and
assigns the new value to D. Of course, both interpretations are equivalent.
From this more object-oriented point of view, a variable declaration, e.g.,
dictionarystring, int D, is creating a new dictionary object with
name D rather than introducing a new variable of type
dictionarystring, int; hence the name ``creation'' for this part of
a specification.
• Operations
In this section the operations of the data types are described. For each
operation the description consists of two parts
a)
The interface of the operation is defined using the function declaration
syntax. In this syntax the result type of the operation (void if there is
no result) is followed by the operation name and an argument list specifying
the type of each argument. For example,
list L.insert (
E x, list
L.insert (
E x, list it, rel
it, rel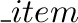 p = after)
defines the interface of the insert operation on a list L of elements of type
E (cf. section 3.7). Insert takes as arguments an element x of type E,
a
list
p = after)
defines the interface of the insert operation on a list L of elements of type
E (cf. section 3.7). Insert takes as arguments an element x of type E,
a
list it and an optional relative position argument p. It returns
a
list
it and an optional relative position argument p. It returns
a
list as result.
E& A[I x]
defines the interface of the access operation on a dictionary array A. It
takes an element of I as an argument and returns a variable of type E.
as result.
E& A[I x]
defines the interface of the access operation on a dictionary array A. It
takes an element of I as an argument and returns a variable of type E.
b)
The effect of the operation is defined. Often the arguments have to
fulfill certain preconditions. If such a condition is violated the effect
of the operation is undefined. Some, but not all, of these cases result
in error messages and abnormal termination of the program (see also
section 7.5). For the insert operation on lists this definition reads:
A new item with contents x is inserted after (if p = after) or before
(if p = before) item it into L. The new item is returned.
(precondition: item it must be in L)
For the access operation on dictionary arrays the definition reads:
returns the variable A(x).
• Implementation
The implementation section lists the (default) data structures used to
implement the data type and gives the time bounds for the operations and
the space requirement. For example,
Dictionary arrays are implemented by randomized search trees ([AS89]).
Access operations A[x] take time
O(log dom(A)).
The space requirement is O(dom(A)).
1.3 Implementation Parameters
For many of the parameterized data types (in the current version: dictionary,
priority queue, d_array, and sortseq) there exist variants taking an additional
data structure parameter for choosing a particular implementation
(cf. section 4). Since does not allow to overload templates we had
to use different names: the variants with an additional implementation
parameters start with an underscore, e.g., _d_arrayI,E,impl.
We can easily modify the example program from section 1.1 to use a dictionary
array implemented by a particular data structure, e.g., skip lists ([Pu89]),
instead of the default data structure (cf. section 4.4.5).
#include LEDA/d_array.h
#include LEDA/impl/skiplist.h
main()
{ &_d_arraystring,int,skiplist N(0);
&string s;
&while &(cin s ) N[s]++;
&forall_defined(s, N)
cout s " " N[s] endl;
}
Any type _XYZ
T1,..., Tk, xyz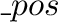 is derived from the corresponding
``normal" parameterized type XYZ
T1,..., Tk, i.e., an instance of type
_XYZ
T1,..., Tk, xyz
is derived from the corresponding
``normal" parameterized type XYZ
T1,..., Tk, i.e., an instance of type
_XYZ
T1,..., Tk, xyz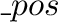 can be passed as argument to functions with
a formal parameter of type XYZ
T1,..., Tk&.
This provides a mechanism
for choosing implementations of data types in pre-compiled algorithms.
See ``prog/graph/dijkstra.c" for an example.
can be passed as argument to functions with
a formal parameter of type XYZ
T1,..., Tk&.
This provides a mechanism
for choosing implementations of data types in pre-compiled algorithms.
See ``prog/graph/dijkstra.c" for an example.
LEDA offers several implementations for each of the data types. For
instance, skip lists, randomized search trees, and red-black trees
for dictionary arrays. Users can also provide their own implementation.
A data structure ``xyz_impl" can be used as actual
implementation parameter for a data type  if it provides a
certain set of operations and uses certain virtual functions for type
dependent operations (e.g. compare, initialize, copy, ...).
Section 9 lists all data structures contained in the current version and
gives the exact requirements for implementations of
dictionaries, priority_queues, sorted sequences and dictionary arrays.
A detailed description of the mechanism for parameterized data types and
implementation parameters used in LEDA can be found in [N92].
if it provides a
certain set of operations and uses certain virtual functions for type
dependent operations (e.g. compare, initialize, copy, ...).
Section 9 lists all data structures contained in the current version and
gives the exact requirements for implementations of
dictionaries, priority_queues, sorted sequences and dictionary arrays.
A detailed description of the mechanism for parameterized data types and
implementation parameters used in LEDA can be found in [N92].
1.4 Arguments
• Optional Arguments
The trailing arguments in the argument list of an operation may be optional.
If these trailing arguments are missing in a call of an operation the default
argument values given in the specification are used. For
example, if the relative position argument in the list insert operation
is missing it is assumed to have the value after, i.e.,
L.insert(it, y) will insert the item y after item it into L.
• Argument Passing
There are two kinds of argument passing in , by value and by reference.
An argument x of type type specified by ``type x'' in the argument
list of an operation or user defined function will be passed by value, i.e.,
the operation or function is provided with a copy of x.
The syntax for specifying an argument passed by reference is ``type& x''.
In this case the operation or function works directly on x ( the variable
x is passed not its value).
Passing by reference must always be used if the operation is to change the
value of the argument. It should always be used for passing large objects
such as lists, arrays, graphs and other LEDA data types to functions.
Otherwise a complete copy of the actual argument is made, which takes time
proportional to its size, whereas passing by reference always takes constant
time.
• Functions as Arguments
Some operations take functions as arguments. For instance the bucket sort
operation on lists requires a function which maps the elements of the list into
an interval of integers. We use the syntax to define the type of a function
argument f:
T (*f )(T1, T2,..., Tk)
declares f to be a function
taking k arguments of the data types T1, ..., Tk,
respectively, and returning a result of type T, i.e,
f : T1×...×Tk→T .
1.5 Overloading
Operation and function names may be overloaded, i.e., there can be different
interfaces for the same operation. An example is the translate operations
for points (cf. section 6.1).
point p.translate(vector v)
point p.translate(
double α, double dist)
It can either be called with a vector as argument or with two arguments
of type double specifying the direction and the distance of the translation.
An important overloaded function is discussed in the next section: Function
compare, used to define linear orders for data types.
1.6 Linear Orders
Many data types, such as dictionaries, priority queues, and sorted sequences
require linearly ordered subtypes. Whenever a type T is used in such a
situation, e.g. in
dictionaryT,... the function
int compare(T, T)
must be declared and must define a linear order on
the data type T.
A binary relation rel on a set T is called a linear order on T if for
all
x, y, z∈T:
1) x rel y
2) x rel y and y rel z implies x rel z
3) x rel y or y rel x
4) x rel y and y rel x implies x = y
A function int
compare(T, T) is said to define the linear order
rel on T if
compare(
x,
y)
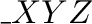
For each of the simple data types char, short, int, long, float,
double, string, and point a function compare is predefined and defines
the so-called default ordering on that type. The default ordering is the
usual ≤ - order for the built-in numerical types, the lexicographic
ordering for string, and for point the lexicographic ordering of the
cartesian coordinates. For all other types T there is no default
ordering, and the user has to provide a compare function whenever a linear
order on T is required.
Example: Suppose pairs of real numbers shall be used as keys
in a dictionary with the lexicographic order of their components.
First we declare class pair as the type of pairs of real numbers,
then we define the I/O operations Read and Print and the
lexicographic order on pair by writing an appropriate compare function.
class pair {
&
double x;
&
double y;
&
pair() { x = y = 0; }
&pair(const
pair& p) { x = p.x; y = p.y; }
&friend void &Read(pair& p, istream& is)
{ is p.x p.y; }
&friend void &Print(const pair& p, ostream& os)
{ os p.x `` " p.y; }
&friend int &compare(const pair&, const pair&);
};
int compare(const pair& p, const pair& q)
{ &if (p.x q.x) return -&1;
&if (p.x q.x) return &1;
&if (p.y q.y) return -&1;
&if (p.y q.y) return &1;
&return 0; }
Now we can use dictionaries with key type pair, e.g.,
dictionarypair,int D;
Sometimes, a user may need additional linear orders on a data type T
which are different from the order defined by compare, e.g., he might
want to order points in the plane by the lexicographic ordering of their
cartesian coordinates and by their polar coordinates. In this example, the
former ordering is the default ordering for points. The user can introduce
an alternative ordering on the data type point (cf. section 6.1) by defining
an appropriate comparing function int cmp(const point&, const point&)
and then calling the macro DEFINE_LINEAR_ORDER(point, cmp, point1).
After this call point1 is a new data type which is equivalent to the data
type point, with the only exception that if point1 is used as an actual
parameter e.g. in
dictionarypoint1,..., the resulting data type
is based on the linear order defined by cmp.
In general the macro call
DEFINE_LINEAR_ORDER(T,cmp,T1)
introduces a new type T1 equivalent to type T with the linear order
defined by the compare function cmp.
In the example, we first declare a function pol and derive a new type
pol
and derive a new type
pol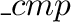 using the DEFINE_LINEAR_ORDER macro.
using the DEFINE_LINEAR_ORDER macro.
int pol (const point& x, cosnt point& y)
{ lexicographic ordering on polar coordinates }
DEFINE_LINEAR_ORDER(point,pol
(const point& x, cosnt point& y)
{ lexicographic ordering on polar coordinates }
DEFINE_LINEAR_ORDER(point,pol ,
pol
,
pol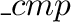 )
)
Now, dictionaries based on either ordering can be used.
dictionarypol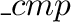 , int D1; &polar ordering
, int D1; &polar ordering
dictionarypoint, int D0; &default ordering
Remark: We have chosen to associate a fixed linear order with most of
the simple types (by predefining the function compare). This order is used
whenever operations require a linear order on the type, e.g., the operations
on a dictionary. Alternatively, we could have required the user to specify a
linear order each time he uses a simple type in a situation where an ordering
is needed, e.g., a user could define
dictionarypoint, lexicographic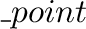 ,...
,...
This alternative would handle the cases where two or more different orderings
are needed more elegantly. However, we have chosen the first alternative
because of the smaller implementation effort.
1.7 Items
Many of the advanced data types in LEDA (e.g. dictionaries), are defined in
terms of so-called items. An item is a container which can hold an object
relevant for the data type. For example, in the case of dictionaries a
dic contains a pair consisting of a key and an information.
A general definition of items will be given at the end of this section.
contains a pair consisting of a key and an information.
A general definition of items will be given at the end of this section.
We now discuss the role of items for the dictionary example in some detail.
A popular specification of dictionaries defines a dictionary as a partial
function from some type K to some other type I, or alternatively, as a
set of pairs from K×I, i.e., as the graph of the function. In an
implementation each pair (k, i) in the dictionary is stored in some location
of the memory. Efficiency dictates that the pair (k, i) cannot only be
accessed through the key k but sometimes also through the location where it
is stored, e.g., we might want to lookup the information i associated with
key k (this involves a search in the data structure), then compute with the
value i a new value i,́ and finally associate the new value with k.
This either involves another search in the data structure or, if the lookup
returned the location where the pair (k, i) is stored, can be done by direct
access. Of course, the second solution is more efficient and we therefore
wanted to provide it in LEDA.
In LEDA items play the role of positions or locations in data structures. Thus
an object of type
dictionaryK, I, where K and I are types, is
defined as a collection of items (type dic ) where each item contains
a pair in K×I. We use k, i to denote an item with key k and
information i and require that for each k∈K there is at most one
i∈I such that k, i is in the dictionary. In mathematical terms this
definition may be rephrased as follows: A dictionary d is a partial
function from the set dic
) where each item contains
a pair in K×I. We use k, i to denote an item with key k and
information i and require that for each k∈K there is at most one
i∈I such that k, i is in the dictionary. In mathematical terms this
definition may be rephrased as follows: A dictionary d is a partial
function from the set dic to the set K×I. Moreover, for each
k∈K there is at most one i∈I such that the pair (k, i) is in d.
to the set K×I. Moreover, for each
k∈K there is at most one i∈I such that the pair (k, i) is in d.
The functionality of the operations
&dic &D.lookup(K k)
&I &D.inf(
dic
&D.lookup(K k)
&I &D.inf(
dic it)
&void &D.change_inf(
dic
it)
&void &D.change_inf(
dic it, I i)́
is now as follows:
D.lookup(k) returns an item it with contents (k, i), D.inf(it)
extracts i from it, and a new value i´ can be associated with k by
D.change_inf(it, i)́.
it, I i)́
is now as follows:
D.lookup(k) returns an item it with contents (k, i), D.inf(it)
extracts i from it, and a new value i´ can be associated with k by
D.change_inf(it, i)́.
Let us have a look at the insert operation for dictionaries next:
&dic &D.insert(
K k, I i)
&D.insert(
K k, I i)
There are two cases to consider. If D contains an item it with contents
(k, i)́ then i´ is replaced by i and it is returned. If D contains
no such item, then a new item, i.e., an item which is not contained in any
dictionary, is added to D, this item is made to contain (k, i) and is
returned. In this manual (cf. section 4.3) all of this is abbreviated to
&
dic D.insert(
K k, I i)
&associates the information i with the key k.
& &If there is an item k, j in D then j is
& &replaced by i, else a new item k, i is added
& &to D. In both cases the item is returned.
D.insert(
K k, I i)
&associates the information i with the key k.
& &If there is an item k, j in D then j is
& &replaced by i, else a new item k, i is added
& &to D. In both cases the item is returned.
We now turn to a general discussion. With some LEDA types XYZ there is an
associated type XYZ of items. Nothing is known about the objects of
type XYZ
of items. Nothing is known about the objects of
type XYZ except that there are infinitely many of them. The only
operations available on
XYZ
except that there are infinitely many of them. The only
operations available on
XYZ besides the one defined in the
specification of type XYZ is the equality predicate ``=='' and the assignment
operator ``='' . The objects of type XYZ are defined as sets or sequences of
XYZ
besides the one defined in the
specification of type XYZ is the equality predicate ``=='' and the assignment
operator ``='' . The objects of type XYZ are defined as sets or sequences of
XYZ containing objects of some other type Z. In this situation an
XYZ
containing objects of some other type Z. In this situation an
XYZ containing an object z∈Z is denoted by z. A new or unused
XYZ
containing an object z∈Z is denoted by z. A new or unused
XYZ is any XYZ
is any XYZ which is not part of any object of type XYZ.
which is not part of any object of type XYZ.
Remark: For some readers it may be useful to interpret a dic as
a pointer to a variable of type K×I. The differences are that the
assignment to the variable contained in a dic
as
a pointer to a variable of type K×I. The differences are that the
assignment to the variable contained in a dic is restricted, e.g., the
K-component cannot be changed, and that in return for this restriction the
access to
dic
is restricted, e.g., the
K-component cannot be changed, and that in return for this restriction the
access to
dic is more flexible than for ordinary variables, e.g.,
access through the value of the K-component is possible.
is more flexible than for ordinary variables, e.g.,
access through the value of the K-component is possible.
1.8 Iteration
For many data types LEDA provides iteration macros. These macros can be
used to iterate over the elements of lists, sets and dictionaries or
the nodes and edges of a graph. Iteration macros can be used similarly to
the for statement. Examples are
for all item based data types:
forall_items(it, D)
{ the items of D are successively assigned to variable it}
for lists and sets:
forall(x, L) { the elements of L are successively assigned to x}
for graphs:
forall_nodes(v, G) { the nodes of G are successively
assigned to v}
forall_edges(e, G) { the edges of G are successively
assigned to e}
forall_adj_edges(e, v) { all edges adjacent to v are
successively assigned to e}
1.9 Header Files
LEDA data types and algorithms can be used in any program as described
in this manual. The specifications (class declarations) are contained
in header files. To use a specific data type its header file has to be
included into the program. In general the header file for data type xyz is
LEDA/xyz.h. Exceptions to this rule are described in Table 10.1 and
10.2.
1.10 Libraries
The implementions of all LEDA data types and algorithms are precompiled and
contained in 5 libraries (libL.a, libG.a, libP.a, libWs.a, libWx.a)
which can be linked with application programs. In the following
description it is assumed that these libraries are installed in one of the
systems default library directories (e.g. /usr/lib), which allows to use
the ``-l...'' compiler option.
a) libL.a
is the main LEDA library, it contains the implementations of all simple
data types (section 2), basic data types (section 3), dictionaries and priority
queues (section 4). A program prog.c using any of these data types has to be
linked with the libL.a library like this:
CC prog.c -lL
b) libG.a
is the LEDA graph library. It contains the implementations of all graph
data types and algorithms (section 5). To compile a program using any graph
data type or algorithm the libG.a and libL.a library have to be used:
CC prog.c -lG -lL
c) libP.a
is the LEDA library for geometry in the plane. It contains the
implementations of all data types and algorithms for two-dimensional
geometry (section 6). To compile a program using two-dimensional data
types or algorithms the libP.a, libG.a, libL.a and maths libraries have
to be used:
CC prog.c -lP -lG -lL -lm
d) libWx11.a, libWxview.a
are the LEDA libraries for graphic windows under the X11 or xview
window systems. Application programs using data type window
(cf. section 6.7) have to be linked with one of these libraries:
a)
For the X11 window system:
CC prog.c -lP -lG -lL -lWx11 -lX11 -lm
b)
For the xview window system:
CC prog.c -lP -lG -lL -lWxview -lxview -lolgx -lX11 -lm
Note that the libraries must be given in the order -lP -lG -lL
and that the window library (-lWx11 or -lWxview) has to appear after the
plane library (-lP).
 I, E) from the library. This is expressed by the include
statement (cf. section 1.9 for more details). The specification of the
data type d
I, E) from the library. This is expressed by the include
statement (cf. section 1.9 for more details). The specification of the
data type d can be found in section 4.4. We use it also as a
running example to discuss the principles underlying LEDA in sections 1.2
to 1.10.
can be found in section 4.4. We use it also as a
running example to discuss the principles underlying LEDA in sections 1.2
to 1.10.
 );
);
 L.insert (
E x, list
L.insert (
E x, list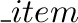 p = after)
defines the interface of the insert operation on a list L of elements of type
E (cf. section 3.7). Insert takes as arguments an element x of type E,
a
list
p = after)
defines the interface of the insert operation on a list L of elements of type
E (cf. section 3.7). Insert takes as arguments an element x of type E,
a
list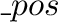 is derived from the corresponding
``normal" parameterized type XYZ
T1,..., Tk, i.e., an instance of type
_XYZ
T1,..., Tk, xyz
is derived from the corresponding
``normal" parameterized type XYZ
T1,..., Tk, i.e., an instance of type
_XYZ
T1,..., Tk, xyz if it provides a
certain set of operations and uses certain virtual functions for type
dependent operations (e.g. compare, initialize, copy, ...).
Section 9 lists all data structures contained in the current version and
gives the exact requirements for implementations of
dictionaries, priority_queues, sorted sequences and dictionary arrays.
A detailed description of the mechanism for parameterized data types and
implementation parameters used in LEDA can be found in [N92].
if it provides a
certain set of operations and uses certain virtual functions for type
dependent operations (e.g. compare, initialize, copy, ...).
Section 9 lists all data structures contained in the current version and
gives the exact requirements for implementations of
dictionaries, priority_queues, sorted sequences and dictionary arrays.
A detailed description of the mechanism for parameterized data types and
implementation parameters used in LEDA can be found in [N92].
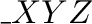
 and derive a new type
pol
and derive a new type
pol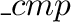 using the DEFINE_LINEAR_ORDER macro.
using the DEFINE_LINEAR_ORDER macro.
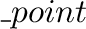 ,...
,...
 besides the one defined in the
specification of type XYZ is the equality predicate ``=='' and the assignment
operator ``='' . The objects of type XYZ are defined as sets or sequences of
XYZ
besides the one defined in the
specification of type XYZ is the equality predicate ``=='' and the assignment
operator ``='' . The objects of type XYZ are defined as sets or sequences of
XYZ